A ideia da esfericidade da Terra não foi muito difícil de aceitar.
A projecção das sombras da Terra na Lua durante
os eclipses parciais e a forma da Lua e do Sol, eram os sinais com que a
Natureza argumentava contra aqueles mundos planos cheios de precipícios para os
infernos.
Os gregos já aceitavam a esfericidade da Terra e
o geógrafo Eratóstenes, que dirigia então a célebre biblioteca de Alexandria,
foi o primeiro a calcular o perímetro do nosso planeta e com um erro bem
inferior a Cristóvão Colon [Salvador Fernando Zarco,1447-1506] 2.000 anos antes deste.
A partir da sombra de um obelisco em Alexandria calculou
que, ao meio-dia do dia do solstício de Verão, o Sol distava do zénite 1/50 da
circunferência. Sabia também que em Siena no Alto -Egipto (hoje em dia Assuão),
naquele dia, o Sol não projectava qualquer sombra nos fundos dos poços ao
meio-dia.
Como as duas cidades estavam aproximadamente no
mesmo meridiano, concluiu assim que o comprimento deste seria 50 vezes a
distância entre elas, distância esta já conhecida.
Com os meios técnicos de então a precisão foi
espantosa. Um erro apenas de 24 Km em 40.000 Km!
Esquema de Eratóstenes para cálculo do
meridiano. Foi talvez a primeira noção de latitude, ainda que não angular.
Atribui-se também a Hiparco a criação do astrolábio, com o qual se mediam alturas, instrumento que os portugueses simplificaram
e adaptaram para o uso náutico.
Ao longo dos tempos outros instrumentos náuticos para tomar alturas foram aparecendo, como o quadrante, a balestilha e finalmente o sextante, cuja precisão de leitura foi sendo melhorada até ao segundo de arco.
Tomando altura de um astro. Não se pode
propriamente falar do problema de latitude à semelhança do da longitude, já que o método de determiná-la era conhecido desde a antiguidade e
não oferecia grandes problemas.
Quando não se avistava terra, as navegações
oceânicas obrigavam ao conhecimento da posição, e como não havia pontos de
referência, foram os astros a servirem esse propósito.
O primeiro terá sido a estrela Polar, pela qual
os portugueses no séc. XV tomavam a altura quando saíam e comparavam dias
depois transformando a diferença da medida do arco em léguas navegadas.
No início um grau equivalia a 16 léguas e 2/3
acertando-se no final do séc. XV para 17,5 léguas por grau. Este método obrigava
a que a tomada da altura fosse feita num determinado momento.
O nocturlábio ou roda polar foi o instrumento usado para se saber as horas e
também fazer as necessárias correcções na leitura, já que no séc. XV a estrela
Polar não estava directamente sobre o pólo e fazia um raio de 3,5º com este.
Devido ao fenómeno de persecução dos equinócios,
este astro encontrava-se num movimento de aproximação do pólo e um século
depois o raio era já bem inferior a 3º. As tabelas tinham de ser sucessivamente
corrigidas ao longo dos tempos.
Este tipo de navegação era conhecido por Regimento do Norte e foi um grande avanço na navegação astronómica. À medida que a navegação se aproximava do Equador a estrela Polar ia desaparecendo sendo a alternativa encontrar outra estrela com propriedades semelhantes.
Este tipo de navegação era conhecido por Regimento do Norte e foi um grande avanço na navegação astronómica. À medida que a navegação se aproximava do Equador a estrela Polar ia desaparecendo sendo a alternativa encontrar outra estrela com propriedades semelhantes.
Como se acha a estrela Polar:
Primeiro localiza-se a constelação da Ursa Maior. ( constituída por um quadrilátero 4 estrelas e uma cauda 3 estrelas). Prolonga-se 5 vezes a distância das estrelas "alpha e
beta", estrelas estas opostas à cauda da constelação, no sentido
da convexidade da cauda.
Encontrará a
Estrela Polar que é a mais brilhante de todas as outras estrelas da Ursa Menor, que é a última estrela da cauda..
A Estrela
Polar indica-nos as imediações do Pólo Norte Geográfico Celeste
No
hemisfério Austral a estrela, Crucis ou Pé do
Cruzeiro, foi usada para o cálculo da latitude, mas a distância daquela
relativamente ao pólo não permitiu cálculos muito rigorosos.
Chegou-se
também a fazer um regimento daquela estrela, mas o cálculo a partir daquela não
era muito do agrado da maioria dos pilotos portugueses.
O
uso da meridiana, tomada da altura do Sol quando este passa no meridiano do
observador, foi o método mais apreciado e fácil qualquer que fosse o
hemisfério. As regras eram simples e já havia tabelas com a declinação para todos os dias do ano. Este método era
conhecido pelo Regimento do Sol.
A Latitude
A latitude é o arco do meridiano que passa no lugar desde o Equador até ao paralelo do lugar.
Conta-se de 0º a 90º a partir do
Equador e é Norte ou Sul conforme o hemisfério terrestre onde se encontra o
lugar.
Nos cálculos a latitude toma valor
positivo a Norte e negativo a Sul.
Para obtermos a latitude de um lugar
temos de tomar a altura do astro (normalmente o Sol ao meio-dia solar, também
chamada de meridiana) e em conjunto com as tabelas náuticas, onde obtemos a declinação do
astro naquele dia, fazemos os cálculos necessários.
Um
meridiano é um círculo máximo que passa por ambos os pólos. Os paralelos,
que devem o seu nome ao facto de serem círculos paralelos ao Equador, marcam as
latitudes.
Cálculo
da latitude através da altura da Polar
por Lusitanian Express, autoria de Luís D. Lopes publicado em:
Culminação
Identificado o momento em que se
verificava a culminação do Sol ou da Polar, na sua direcção (azimute) ou na
direcção oposta encontrava-se o Norte (ou o Sul) Geográfico. Com o nascimento
da navegação astronómica, a identificação do momento da culminação tinha como
objectivo a determinação da latitude do lugar. Através da altura observada
exactamente no momento da culminação da Polar ou do Sol, utilizando o
quadrante, o astrolábio ou a balestilha, e após cálculos relativamente simples,
era possível determinar a latitude do lugar onde se encontrava o observador.
O
cálculo da latitude do lugar, utilizando a altura do Sol e da Polar, exigia que
se determinasse com precisão o momento em que se verificava a culminação
(passagem pelo meridiano do lugar) do Sol e da Polar.
Com a introdução da navegação astronómica,
o conhecimento do momento da culminação do Sol ou da Polar era crítico e é
precisamente na tentativa de identificação desse momento que os navegadores se
apercebiam das diferenças, mais ou menos significativas, que se verificavam
entre o norte magnético e o norte verdadeiro.
Já era conhecido o facto que as agulhas
nem sempre estarem fixas nos pólos, pelo que a identificação sistemática ou a evidência da
existência de um ângulo entre o norte da agulha (norte magnético) e o azimute
observado nas culminações do Sol e da Polar (norte geográfico), que surgiu
como consequência dos processos utilizados para o cálculo da
latitude, veio consolidar o conhecimento sobre esse afastamento, nomeadamente a
percepção, obtida com a sequência de observações, que esse afastamento era
variável conforme o lugar geográfico.
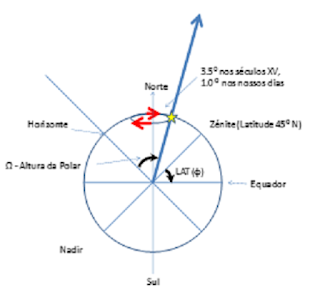
A Estrela Polar - Cálculo da latitude do
lugar
Recordemos que a distância angular da
Polar em relação ao Pólo era bem maior nos séculos XV e XVI do que aquela que
se observa nos nossos dias, sendo então aproximadamente igual a 3.5 graus.
fig.
nº 1 – Passagem meridiana da Polar
A passagem meridiana do Sol coincide com a
sua altura máxima sobre o horizonte, quanto à Polar (estrela só visível
no hemisfério norte), a utilização dos Regimentos permitiu ultrapassar a
dificuldade da determinação da sua passagem meridiana, considerando que esta
acontece duas vezes por dia.
No exemplo da fig. nº 1, e para a
passagem meridiana da Polar correspondente ao valor máximo que se observa para
a altura da Polar sobre o horizonte, facilmente se conclui o seguinte:
(século XV)
Latitude (φ) = 90º - (90º - Ω (altura) ) –
3.5º = Ω (altura) - 3.5º
(nossos dias)
Latitude (φ) = 90º - (90º - Ω (altura) ) –
1º = Ω (altura) – 1º
fig.
nº 2 – Passagem meridiana da Polar
No exemplo da fig. nº 2, e para a segunda
passagem da Polar pelo meridiano do lugar, também facilmente se conclui o
seguinte:
(século XV)
90º - Latitude (φ) = 90º - (90º - Ω
(altura) + 3.5º) = Ω (altura) + 3.5º
(nossos dias)
90º - Latitude (φ) = 90º - 90º - Ω
(altura) + 1.0º) = Ω (altura) + 1.0º
Com os exemplos das figuras nº10 e nº 11,
concluímos que a latitude de um lugar, através da altura da estrela Polar,
seria igual à altura observada corrigida por um factor situado no intervalo
[-3.5º, +3.5º].
(século XV)
Latitude (φ) = Ω (altura) + [- 3.5º, +
3.5º]
A determinação deste factor de correcção
esteve precisamente na origem dos vários Regimentos da Polar que surgiram na
época dos Descobrimentos.
É interessante notar que um erro na
aplicação deste factor podia levar a ocorrência de erros de cálculo da latitude
na ordem dos sete graus, o que já seria um erro muito grosseiro, mesmo para a
época.
“E sabereis que quando as
guardas estiverem em a cabeça, [*] está três graus mais abaixo do eixo [**];
outro tal quando as guardas estão ao pé do norte, então o norte está três graus
mais alto que deve acima do eixo”
[*] – Polar
[**] – Pólo
(Reportório dos Tempos, edição de
1563)
Ou ainda
“E sabereis que quando as guardas
estiverem em a cabeça, está a estrela abaixo do Pólo três graus ………………. quando
as guardas estão na linha acima do braço de oeste está a estrela abaixo do Pólo
meio grau”
(Guia Náutico de Munique,
edição de 1509)
Numa fase inicial de utilização da estrela
Polar pelos navegadores, estes utilizavam-na acima de tudo como referência,
através de simples processos de comparação de alturas. Registavam a altura da
Polar nos vários lugares por onde passavam, deste modo podiam avaliar a
distância meridiana (16,17 ou 18 léguas por grau de latitude, conforme a
época e a evolução do conhecimento sobre as dimensões do nosso planeta) a que
se encontravam do paralelo do ponto de referência.
Por exemplo, registavam a altura da
Polar em Finisterra, em Lisboa, nas Canárias, em Cabo Verde, no Funchal, etc.
Encontrando-se a embarcação num lugar em que se observava a Polar por uma
determinada altura, podiam avaliar a distância em latitude face
a um desses pontos de referência.
Para medir a altura dos astros, os antigos
navegantes começaram por usar o quadrante e o astrolábio náutico, instrumentos
que têm a vantagem de não necessitar do horizonte, uma vez que medem a
distância zenital de qualquer astro, ângulo entre a direcção do astro e o
zénite. Como a distância zenital é a complementar da altura, esta podia ser
obtida pela subtracção para 90°.
Quadrante
fig.
nº 3 – Quadrante
“Partindo alguém de Lisboa
paramentes onde lhe cai a chumbada….e põe ali um sinal sobre o quadrante, em
tal tempo que as estrelas da guarda estão leste-oeste com a estrela do Norte”
(Reportório dos Tempos, edição de
1563)
Portanto era sugerido ao navegador que
marcasse no próprio quadrante o valor do ângulo definido pelo pêndulo
(chumbada), que era a altura da Polar em Lisboa para uma determinada posição
das guardas.
“E depois de um ou dias de mar,
quando quer que quiserdes saber no mar quanto o vosso navio está diferenciado
de Lisboa, verás a quantos graus vos cairá o chumbo, ou de um lado ou do outro
do vosso primeiro ponto [Lisboa] ”
Obtida a diferença entre as duas alturas,
bastava multiplicar esta diferença pelo número de léguas por grau, para se obter
as distâncias, em latitude, entre lugares. Este método designa-se por método
de comparação de alturas.
Podemos então concluir que numa primeira
fase, com a introdução dos regimentos pretendia-se obter valores correctos nas
comparações de alturas, e só numa fase posterior é que se iniciou a
determinação das latitudes dos lugares.
fig.
nº 4 – Ursa Menor e a Polar
Na figura nº 4, apresentamos de forma
simplificada a trajectória que a Polar descreve nos céus para um observador
situado num lugar situado no hemisfério norte e olhando em direcção ao norte
geográfico. Os regimentos da época dos descobrimentos faziam referência
precisamente a determinadas posições visuais que as estrelas da constelação da
Ursa Menor (nomeadamente as guardas) assumiam.
fig.
nº 5 – A Polar
Com melhor
detalhe, tendo como referência a figura nº 5, na qual tentamos representar o
movimento aparente da Polar nos céus de um determinado lugar no hemisfério
norte, podemos concluir o seguinte:
A posição 1
representa a altura máxima alcançada pela Polar, se não
fosse utilizado nenhum factor de correcção a latitude calculada
seria superior à do local .
A posição 3
representa a altura mínima alcançada pela Polar, se não fosse utilizado
nenhum factor de correcção a latitude calculada seria inferior à
do local .
Para as
posições 2 e 4, a altura observada pode ser considerada como igual à latitude
do lugar.
O momento da
leitura da altura [ex: em tal tempo que as estrelas da guarda estão
leste-oeste com a estrela do Norte] era crítico para o rigor do
processo. Numa primeira fase seriam as observações visuais que garantiam o
respeito pelas regras definidas pelos regimentos ou simples conhecimentos que
iam sendo transmitidos entre os pilotos. Mais tarde, seguramente com o início
da utilização do Sol na navegação astronómica, surgiram mecanismos cuja
utilização associada à agulha de marear permitia a determinação mais rigorosa
do momento em que se pretendia obter a altura de um determinado astro.
Nota de
Rodapé
O Astrolábio
náutico terá sido provavelmente uma adaptação do astrolábio planisfério. Em
1664, Hooke transforma o astrolábio, adicionando-lhe um jogo de espelhos o que
permitia a observação simultânea do astro observado e da linha do
horizonte. Newton, em 1669, reduz o semicírculo graduado, em 1742, Hadley
transforma ainda mais o astrolábio e, em 1757, Campbell inventa o Sextante.
Em 1919, Gago
Coutinho descreveu pela primeira vez o sistema de horizonte artificial o qual
incluía um nível de bolha embutido na estrutura de um sextante
convencional. O Sextante de horizonte artificial é um dispositivo
de navegação aérea utilizado para a medição da altura de um astro sem
que seja necessário recorrer ao horizonte.
por Lusitanian Express, autoria de Luís D.
Lopes publicado em: 19.02.19
Repetindo o processo utilizado quando
estudámos o caso da Polar, no exemplo da fig. nº 16, na qual se pretende
representar o momento da passagem meridiana do Sol em um determinado lugar com
latitude do mesmo sinal que a declinação do Sol, facilmente se conclui o
seguinte:
Latitude (φ) = 90º - Ω (altura do Sol em
relação ao horizonte) + declinação (δ)
fig. nº 6 – Passagem meridiana
do Sol (latitude e declinação NORTE)
No exemplo da fig. nº7, com latitude e
declinação de sinal diferente
fig. nº7 – Passagem meridiana do Sol
(latitude NORTE e declinação SUL)
verificamos o seguinte:
Latitude (φ) = 90º - Ω (altura do Sol em
relação ao horizonte) - declinação (δ)
Podemos então concluir que nas passagens
meridianas do Sol, temos a seguinte igualdade:
Latitude = (90º - altura observada do Sol
em relação ao horizonte) ± Declinação (*)
(*) + se a declinação for
do mesmo sinal da latitude (Norte ou Sul) , - no caso oposto
Para sermos rigorosos, devemos acrescentar
que a altura observada do Sol (seja qual for o instrumento utilizado) em
relação ao horizonte deveria ser sujeita a pequenas correcções, todas elas
obviamente ignoradas no tempo dos Descobrimentos. Desse conjunto de correcções
destacamos as seguintes:
Altura do observador em
relação ao solo/mar (conhecido no meio náutico por "dip")
Refracção da luz (Sol,
Lua, Marte, etc) quando esta atravessa a atmosfera terrestre
Semi-diâmetro do astro observado. Todas as efemérides astronómicas
consideram o centro geométrico do astro observado. No caso do Sol e da Lua, o
semi-diâmetro é significativo e deverá ser efectuada uma correcção sempre
que se observa a altura do limbo inferior (situação mais normal, só
excepcionalmente se utiliza o limbo superior ou o centro).
Deve ser reforçado que estas correcções (e
outras aqui não identificadas) são geralmente muito pequenas, absolutamente
irrelevantes na época dos Descobrimentos.
Como então identificar o momento da
passagem do Sol pelo meridiano do lugar?
Existe um processo prático que nos permite
eliminar a necessidade de identificarmos antecipadamente e com muita
precisão, o momento exacto da culminação. Este processo baseia-se na
leitura sucessiva de alturas do Sol (trânsito do Sol) quando se presume que o
momento da culminação esteja próximo. Este processo era (e é) muito utilizado,
e exige que durante alguns minutos o navegador obtenha e registe sucessivas
alturas do Sol sobre o horizonte. Após a passagem pelo meridiano do lugar, a
altura observada do Sol começa a diminuir, o que significa que para aquele
lugar o valor máximo para a altura do Sol já foi alcançado.
A altura máxima observada (que foi
registada pelo observador) corresponde ao momento da passagem meridiana e será
esse o valor utilizado nos cálculos. O erro resultante deste processo é
absolutamente aceitável excepto se o navegador for extremamente inábil.
fig. nº 8 – Determinação da passagem
meridiana do Sol
Passagem meridiana do Sol
Na época dos Descobrimentos foram
utilizados diversos mecanismos que tinham como objectivo a determinação da
passagem meridiana do Sol. Estes mecanismos surgem com a crescente utilização
do Sol na navegação astronómica, sendo mais tarde adaptados, com objectivos
diferentes, para o processo(*) de determinação da longitude e para a
determinação da declinação magnética.
(*) - Como teremos oportunidade de abordar
num outro texto, João de Lisboa, no seu célebre Tratado da Agulha de
Marear (1514), formulou uma (falsa) teoria que pretendia estabelecer uma
relação directa entre o afastamento das agulhas face ao norte geográfico e a
longitude.
Um desses mecanismos consistiria num
semicírculo de latão pouco espesso, que era montado sobre a caixa da
agulha de modo que o seu plano ficasse perpendicular ao da agulha de marear.
Para fazer a observação, o semi-disco era orientado de forma a garantir
que não projectasse sombra para qualquer dos lados, tentando fazer coincidir
esse momento com o da passagem do Sol pelo enfiamento do semi-disco com a
flor-de-lis. Ignorando a existência da declinação magnética, considerava-se que
a passagem meridiana do Sol (o meio-dia solar) se verificava nesse momento,
devendo então ser obtida a altura do Sol sobre o horizonte.
fig. nº 9 – Determinação da
passagem meridiana do Sol através da sombra
Na realidade, na grande maioria das
situações este procedimento não funcionava ou fornecia valores errados, pois se
a declinação magnética fosse diferente de zero, a passagem meridiana do Sol não
se verificava quando o Sol passasse pelo enfiamento com a flor-de-lis, isto
porque o norte magnético não coincidia com o norte geográfico.
Como consequência, a máxima altura
observada do Sol sobre o horizonte não se verificava naquele momento, o do enfiamento
do Sol com a flor-de-lis. Sempre que a declinação magnética fosse diferente de
zero, a altura máxima verificava-se antes ou depois da passagem do Sol pelo
enfiamento com a flor-de-lis. Se esta situação fosse ignorada/desprezada ou
desconhecida, os valores calculados para a latitude poderiam estar
consideravelmente errados.
Na figura nº 10 tentamos ilustrar uma
situação em que a altura máxima acontece depois da passagem do
Sol pelo enfiamento com a flor-de-lis. Nesta situação, a altura observada (e
utilizada no cálculo da latitude) é menor que a altura do Sol
na sua passagem pelo meridiano do lugar. Claro que a situação de erro daqui
resultante é em tudo semelhante caso a altura máxima aconteça antes da
passagem do Sol pelo enfiamento com a flor-de-lis (figura nº 11).
fig. nº 10 – Altura máxima do Sol depois da
sua passagem pela flor-de-lis
fig. nº11 – Altura máxima do Sol antes da
sua passagem pela flor-de-lis
Quando a declinação magnética não era
nula, independentemente de ser Leste ou Oeste, o valor da altura do Sol
considerado para os cálculos era sempre inferior ao valor
obtido no momento passagem do Sol pelo enfiamento com a flor-de-lis.
Quanto maior fosse o valor da declinação magnética maior seria o erro no
cálculo do valor da latitude, isto porque a diferença entre o valor da altura
do Sol considerado para efeito dos cálculos da latitude e a altura máxima que o
Sol atingia no seu trânsito, seria também mais significativa.
O trânsito do Sol implicava a
observação da sua altura de um modo continuado, até a que mediclina do
astrolábio acusa-se a sua máxima inclinação (se fosse o astrolábio o
instrumento utilizado).
Suspendendo o astrolábio náutico pela
argola, orientava-se na direcção do Sol e rodava-se a mediclina de
maneira que a luz do Sol passasse pelos dois orifícios simultaneamente e
tomava-se nota das leituras dos quadrantes graduados indicados pela mediclina.
Uma vantagem de usar o astrolábio náutico para observar o Sol era este não ser
observado directamente, não havendo, portanto, perigo para a vista dos
observadores (ao contrário do quadrante).
Em 1532, ano em que foi editado o
"Tratado del Sphera y del Arte de Marear", de Francisco
Faleiro, a dificuldade neste processo era reconhecida por Francisco
Faleiro, quando afirma que era necessário
«muita vigilância em conhecer
pontualmente o meio-dia, porque tudo o que se errar em conhecê-lo, se errará na
conta deste instrumento».
Em Lisboa, por volta do ano 1500, a
declinação magnética era pouco significativa, cerca de 3º graus leste, e
na Guiné, por andava Mestre José, a declinação ainda seria menor, quase
nula. Este valor deveria ser, no máximo aproximadamente ¼ de quarta, por isso a
sua leitura deveria ser extremamente difícil, eventualmente até poderá não ter
sido detectado nesta fase inicial de estudo e testes, dado o seu valor absoluto
ser tão pequeno.
Concluímos então, que para valores
pequenos de declinação magnética, o valor do erro cometido nos cálculos da
latitude, por não ser considerado o valor da altura do Sol na sua culminação,
era muito pequeno, podemos mesmo dizer desprezável.
Por outro lado, não devem ser ignoradas as
naturais dificuldades na obtenção das alturas dos astros durante as viagens,
não só as criadas pelas condições de mar e visibilidade mas também as
resultantes do nível rudimentar da qualidade técnica e operacional dos
instrumentos de então (quando comparados com os sextantes dos nossos dias).
O astrolábio encontrava-se graduado em
graus (um grau é equivalente a 60 minutos), pelo que a interpolação visual
entre graus dependia muito do observador. Tendo em consideração a escala que se
observa na figura, e ignorando as dificuldades já identificadas no processo de
leitura das alturas dos astros, podemos afirmar que as alturas observadas,
considerado apenas a componente técnica do instrumento utilizado, teriam um
erro (resultante da interpolação da escala) que se situava num intervalo de
cerca de 15 minutos (*).
(*) - um minuto de latitude equivale a
1852 metros, ou seja, uma milha náutica. Como exemplo, um erro de 10 minutos na
altura observada do Sol na sua passagem meridiana é equivalente a 10 milhas
náuticas / 18.520 metros de erro em latitude.
Como nota final, consideremos os seguintes
valores observados em Lisboa, a 22 de Fevereiro de 2018, para a altura do Sol:
1244 - 41º 18'
1247 - 41º 19'
1250 - 41º 20' (meio-dia solar -
culminação)
1253 - 41º 19'
1256 - 41º 18'
Facilmente concluímos que as variações
observadas na altura do Sol seriam totalmente imperceptíveis para os
nossos marinheiros da época, isto considerado o intervalo de erro de 15 minutos
já identificado.
Através de uma simples leitura da
agulha de marear e respectivo aparelho de sombras, os pilotos sabiam que o
meio-dia solar ia acontecer dentro de alguns minutos. Começavam a obter alturas
sucessivas do Sol procurando determinar o valor máximo. Os pilotos mais
atentos, ao utilizarem o método das alturas sucessivas, tinham a possibilidade
de verificar que em algumas situações (declinação magnética pronunciadamente
diferente de zero) o Sol continuava a “subir”, isto apesar de já ter passado
pelo enfiamento da flor-de-lis, ou que começava a “descer” ainda antes da
passagem do Sol pelo enfiamento da flor-de-lis. Os pilotos podiam
assim concluir que as agulhas “não estavam fixas nos pólos”, e numa
fase posterior iriam acabar também por perceber que os ângulos observados
para esse afastamento variavam com os lugares por onde os navios passavam.
A altura
máxima observada para o Sol tinha sido observada num momento em que o Sol não
estava alinhado com os Pólos, o meridiano do lugar não coincidia com o
meridiano definido pelos pólos da agulha magnética.
É fácil pois concluir que, na sequência da
introdução da utilização do Sol na navegação astronómica, os pilotos começaram
a aperceber-se do fenómeno da declinação magnética embora não o compreendessem.
Nota de rodapé
Outros métodos de sombras
Merece especial referência a existência de
outros métodos de sombras que já no século XVI eram utilizados. Um deles
consistia na projecção da sombra de um estilete cravado no centro da
tampa da caixa da agulha, «uma, duas ou três horas antes do meio-dia, e
outro tempo depois do meio-dia». A bissectriz do ângulo determinado
pelas duas sombras correspondentes do estilete definia naturalmente a linha
Norte-Sul geográfica do lugar; a distância angular dessa linha ao plano
vertical que continha a agulha de marear era a declinação magnética. Como o controlo
do tempo não era muito rigoroso, outro método alternativo consistia nas
observações da sombra para alturas iguais durante o trânsito ascendente e
descendente, isto porque o Sol, antes e depois da sua passagem meridiana,
atinge duas vezes a mesma altura acima do horizonte. A autoria destes métodos
relacionados com a obtenção da bissectriz é geralmente atribuída a Pedro Nunes.
(em termos astronómicos, este método
ignora a evolução contínua da declinação do Sol mas os efeitos desta variação
são absolutamente residuais nos métodos aqui apresentados)
O Norte Geográfico
O Sol
por Lusitanian Express, em 22.03.16
O Sol
por Lusitanian Express, em 22.03.16
autoria de Luís D. Lopes publicado em:
O Sol
O Sol
20.02.18
Existem vários processos que permitem determinar
com precisão a direcção do Norte geográfico. Alguns desses processos são muito
antigos, já utilizados nas primeiras civilizações, como a grega ou egípcia por
exemplo, nomeadamente através das culminações do Sol e da estrela Polar, embora
a utilização desta última assentasse num processo de maior complexidade. Neste
capítulo vamos abordar o processo de utilização do Sol na determinação do Norte
geográfico.
Comecemos por referir que a projecção
vertical de um observador na esfera celeste é o seu Zénite. Na direcção oposta
encontra-se o Nadir.
O movimento aparente do
Sol
Durante o percurso aparente que o Sol descreve no céu
num determinado lugar de observação, o Sol irá atingir a altura máxima em
relação ao horizonte quando cruzar o meridiano (longitude) desse lugar. Nesse
momento, o meio-dia solar, o Sol culmina nos azimutes
(direcções) norte ou sul, dependendo da latitude do lugar e da declinação do
Sol.
A declinação do Sol
Ao longo do ano, o Sol descreve um movimento aparente
face ao equador que se situa entre os 23⁰ 27´N e os 23⁰ 27´S (valores aproximados), constituindo os
valores extremos os solstícios e os valores nulos (quando o movimento aparente
do Sol cruza o equador) os equinócios.
Esse ângulo em relação ao Equador chama-se declinação (δ)
e tem influência directa na forma como vemos o Sol descrever o seu movimento
aparente no Céu ao longo do ano.
Um observador situado em Lisboa, e olhando para Sul,
nos equinócios e nos solstícios verá o Sol descrever os movimentos que
exemplificamos na figura nº 4. Todos os percursos (arcos) aparentes que o Sol
descreve no Céu ao longo do ano estão situados entre os arcos extremos, ou seja
aqueles que são percorridos pelo Sol durante os solstícios.
Os azimutes no nascimento e no ocaso são obviamente
diferentes mas no caso de Lisboa o Sol culmina (altura máxima sobre o
horizonte) sempre a Sul.
Fig. nº4 – Movimento aparente do Sol ao
longo do ano nos céus de Lisboa
Quando o Sol se encontra no Solstício de Verão, ou
seja com declinação (δ) igual a 23 º 27’ Norte, o Sol nasce em
Lisboa pelo azimute 059º e o ocaso é pelo azimute 301, pelo que estamos perante
o maior dia do ano. O inverso acontece no solstício de Inverno, com o Sol a
nascer pelos 120º e o ocaso a acontecer 240º, constituindo assim a maior noite
do ano. Nos equinócios (declinação nula), a duração dos dias é igual à das
noites.
Norte-Sul
Na figura 5, as setas a vermelho identificam o
caminho aparente do Sol quando está acima do horizonte.
Fig. nº5 – Passagem meridiana do Sol
Num lugar cuja latitude é 45⁰ Norte, um observador situado nesse lugar verifica que o Sol
cruza o meridiano do observador sempre no
azimute (direcção) igual a Sul (180⁰). O momento da
passagem do Sol pelo meridiano é aquele em que o Sol atinge máxima altura sobre
o horizonte, o meio-dia solar (fig. nº6).
Fig. nº6 – Passagem meridiana do Sol
Na figura 7, apresentamos um outro exemplo em relação
às passagens meridianas do Sol, mas desta vez com o Sol a culminar a norte. As
setas a vermelho identificam novamente o caminho aparente do Sol quando
está acima do horizonte.
Fig. nº7 – Passagem meridiana do Sol
Num lugar cuja latitude é 45⁰ Sul, um observador situado nesse lugar verifica que o sol
cruza o meridiano sempre no azimute (direcção) Norte
(360⁰). (fig. nº8)
Fig. nº8 – Passagem meridiana do Sol
A Estrela Polar
por Lusitanian Express,
autoria de Luís D. Lopes publicado em:
http://cabodastormentas1488.blogs.sapo.pt/4-2-a-estrela-polar-2470,
A utilização da estrela Polar na determinação da direcção do norte
geográfico aparenta ser um processo mais simples mas não é exactamente assim.
De facto, dizer que a Polar está sempre na direcção do norte geográfico não é
rigorosamente verdade.
Como primeira dificuldade na utilização da estrela Polar
para este efeito, é o facto de a estrela Polar só ser visível no hemisfério
Norte, isto em termos astronómicos, pois na prática só é visível para latitudes
superiores aos 5-10 graus norte, a identificação visual da Polar é muito
difícil em latitudes (norte) que se aproximam do Equador.
Como segunda dificuldade, e para sermos rigorosos, sabemos que
a Polar não se encontra exactamente no enfiamento do eixo da Terra,
apresentando uma distância angular de cerca de um (1) grau, pelo que a Polar
descreve um pequeno círculo no céu em cada dia. A orientação do eixo da Terra
está directamente ligada ao fenómeno da Precessão dos Equinócios.
Precessão dos Equinócios
O efeito da atracção que o Sol e Lua exercem sobre o nosso planeta,
que não é uma esfera perfeita, provoca um movimento da projecção do eixo da
Terra ao longo de uma circunferência, movimento conhecido por precessão
dos equinócios, pelo que esta distância angular varia ao longo dos tempos.
Em termos práticos podemos visualizar a precessão dos equinócios da Terra
através do movimento que se observa num pião que roda com o seu eixo
ligeiramente inclinado.
Na figura anterior podemos identificar o referido movimento de precessão do
eixo da Terra. Cada volta completa tem uma duração aproximada de 26.000 anos.
A precessão afecta a direcção do eixo da Terra, mas não afecta o ângulo de
inclinação em relação à eclíptica, que se mantém constante (*).
Devido ao movimento de precessão, a distância angular da Polar em
relação ao Pólo era bem maior nos séculos XV e XVI do que aquela que se
verifica nos nossos dias, sendo então aproximadamente igual a 3.5 graus. Dentro de 14.000 anos, a estrela Vega será a estrela Polar.
Como a Polar não se encontra exactamente no enfiamento do eixo da Terra, ao
descrever aparentemente um círculo no céu, a Polar passa no meridiano do lugar
do observador duas vezes por dia.
Na época dos Descobrimentos tentou-se ultrapassar esta dificuldade através
dos célebres Regimentos (existem vários) da Estrela Polar que os pilotos
utilizavam a bordo. Podemos dizer que um Regimento de então correspondia aos
guias práticos dos nossos dias.
Com a utilização destes regimentos pretendia-se determinar, com o
rigor possível, o momento da passagem meridiana da Polar, obtendo-se um factor
de correcção a considerar no cálculo da latitude do lugar de observação da
Polar (como veremos detalhadamente num outro capítulo).
Resumindo, identificado o culminar da Polar, o seu azimute nesse momento
será sempre Norte e a Polar passará duas vezes por dia pelo meridiano do
observador (fig. nº9).
Fig. nº9 – Passagem meridiana da Polar
Hoje, o eixo da Terra está
inclinado cerca de 23º 27' graus em relação ao plano da sua órbita em torno do
Sol. Mas esta inclinação não é constante, variando entre 22,1 e 24,5 graus
durante um ciclo aproximadamente igual a 40.000 anos. Esta variação é o resultado
de perturbações planetárias do próprio Sistema Solar onde a Terra se encontra
integrada
Cálculo da Declinação do Sol no tempo dos Descobrimentos
por Lusitanian Express, em 22.03.16
Como explicado no capítulo




(*) - Notas adicionais
(Obliquity
of the ecliptic for 20,000 years, from Laskar (1986). O ponto vermelho
representa o valor da inclinação do eixo da Terra no ano 2000)
Existe ainda o movimento de nutação, que é uma oscilação muito
pequena do eixo de rotação da Terra, cerca de 9 segundos de arco
durante um curto período de aproximadamente 18.6 anos. O centro de gravidade do
sistema Terra-Lua não coincide com o centro de gravidade da Terra, daqui
resultando a oscilação conhecida como nutação.
Cálculo da Declinação do Sol no tempo dos Descobrimentos
autoria de Luís D. Lopes publicado em: Cabo das Tormentas 1488
14.01.19
Para o cálculo da latitude, o navegador tinha que conhecer o valor da declinação do Sol no momento em que obtinha a altura do Sol na sua culminação. O cálculo da declinação era um problema vincadamente matemático, tendo os astrónomos da época optado por construir tabelas/tábuas com o objectivo de serem utilizadas pelos Capitães e Pilotos.
Dois anos antes do início da viagem de Bartolomeu Dias (1487), temos uma indicação clara que o processo de obtenção da latitude através da altura do Sol, na sua culminação, estaria a ser testado e verificado pelos portugueses para posterior utilização por parte dos seus navegantes. Diogo Cam, eventualmente na sua segunda viagem em 1485, já terá utilizado tábuas de declinação do Sol.
Numa nota escrita por Cristóvão Colon num seu exemplar do Imago Mundi de Pierre d’Ailly, sabemos que em 1485, Mestre José Vizinho, medido e astrólogo da corte de D. João II, viajou para a Guiné para “reconhecer a altura do Sol em toda a Guiné”. José Vizinho será provavelmente o autor da "Tábua Solar Única" do Manual de Munique, impressa em 1504, trabalho baseado no Almanach Perpetuum de Abraão Zacuto, astrónomo português, judeu, nascido em Salamanca.
O Almanach Perpetuum Celestium Motuum, que foi elaborado entre 1473 e 1478, era constituído por um conjunto de tábuas astronómicas de diversos tipos e para diversos fins, e foi preparado para o ano de 1473, o que significa que os valores inscritos nas suas tabelas estavam calculados para esse ano, sendo necessário fazer correcções quando se pretendia conhecer os valores dos elementos tabelados para qualquer ano posterior aos períodos fixados nas tabelas.
O Almanach Perpetuum Celestium Motuum foi reeditado e impresso tipograficamente em Leiria em 1496, tendo sido traduzido do hebreu para o latim e para o castelhano por Mestre José Vizinho. Neste livro foram publicadas as tábuas astronómicas para os anos de 1497 a 1500.
Devido ao fenómeno da precessão dos equinócios já aqui falado, o eixo da Terra completa uma volta em cerca de 26.000 anos. Apesar de muito lento para a escala humana, em termos astronómicos equivale aproximadamente a um arco de um (1) minuto por ano, daqui resultando que os valores das tábuas de declinação eram apenas válidos para um ano específico. Considerando todas as condicionantes envolvidas no cálculo da latitude, como por exemplo a qualidade técnica dos instrumentos utilizados (como já referido, a leitura de um ângulo através de um astrolábio ou quadrante tinha associado um erro de interpolação na ordem de 15 minutos), ou as condições de tempo e mar, concluímos que o efeito nos resultados dos cálculos de eventuais erros nos valores considerados para a declinação do Sol seriam quase nulos.
O grau de precisão oferecido por estas tábuas era excepcional, fazendo com que fossem utilizadas como base de diversas outras tábuas destinadas aos marinheiros, como as várias tábuas solares quadrienais (com dados válidos para quatro anos) calculadas e publicadas em Portugal até à publicação das tábuas do Sol de Pedro Nunes de 1537.
A utilização da tábua solar era explicada no Manual de Munique da seguinte forma:
Tábua Solar Única (Março) do Manual de Munique
O Zodíaco é composto por 12 signos que o Sol percorre no seu movimento aparente ao longo do ano. Daqui resulta que cada signo corresponde a 30 graus de arco (360 graus / 12) . Por sua vez, uma órbita completa da Terra em roda do Sol tem uma duração aproximadamente igual a 365,24 dias (365 dias e seis horas) pelo que o Sol, no seu movimento aparente de translacção, percorre um arco ligeiramente superior a um grau em cada dia de calendário.
Na construção da tábua supra (1504), um grau de signo é ligeiramente menor que um dia, tal como se verifica na coluna escrita a negro (segunda coluna a contar da esquerda). A primeira coluna escrita a vermelho representa os dias do mês de Março (*).
Tentando avaliar o rigor da Tábua Solar do Manual de Munique, procedemos ao cálculo, para 1504, dos seguintes valores (em graus) da declinação do Sol:
(para o cálculo da declinação solar, utilizei o seguinte link
9 de Março - 0,47 Sul
10 de Março - 0,08 Sul
11 de Março - 0,32 Norte
12 de Março - 0,71 Norte
Para as datas identificadas, os valores da declinação alteravam diariamente cerca de 0,4 graus (24 minutos). Consultando a 4ª coluna da tabela (contando da esquerda para a direita), verificamos que os valores registados na tábua coincidem com os valores calculados e que 24 minutos é exactamente o valor utilizado para o intervalo entre minutos de declinação tabelados.
Não sabemos se era feita alguma interpolação na leitura dos valores da declinação, assumimos mesmo que o valor utilizado nos cálculos náuticos (ver capítulo anterior, - Cálculo da latitude através da altura do Sol) era o que resultava da leitura directa da tábua para um determinado dia, sem qualquer interpolação.
Ao avaliar o grau de precisão nos cálculos efectuados, podemos então afirmar que o erro máximo no valor obtido para a declinação seria na ordem dos 24 minutos. Se a este valor adicionarmos o valor de 15 minutos, representado este o erro máximo na leitura da escala do astrolábio, obtemos o valor de 39 minutos. Podemos então concluir o seguinte:
O erro máximo no cálculo da latitude através da altura do Sol, no final do século XV e início do século XVI, considerando factores condicionantes tais como as tábuas náuticas utilizadas nos cálculos para a declinação e os instrumentos de leitura da altura do Sol, seria seguramente inferior a um grau, o que consideramos, tendo em consideração os referidos factores condicionantes, como excelente.
Nota de rodapé
(*)
É curioso notar que a tabela apresenta um erro, tal como anotamos na figura. Os graus de cada signo são 30 e não 29, valor que surge registado na tabela (dia 9/10 de Março) na entrada em Carneiro. Esse erro é corrigido, de forma engenhosa, por quem escreveu esta tabela, ao duplicar, para os dias 16 e 17 de Março, o grau 6.
por Lusitanian Express,autoria de Luís D. Lopes publicado em: Cabo das Tormentas 1488
Como explicado no capítulo
Cálculo da latitude
através da altura do Sol, o navegador, para efectuar o cálculo da
latitude, tem que conhecer simultaneamente o valor da altura do Sol em relação
ao horizonte e a sua declinação, isto no exacto momento em que este culmina.
Conhecida
estes valores, sabemos que é possível estabelecer a seguinte igualdade:
Latitude = (90º - altura observada do Sol em relação ao horizonte) ±
Declinação (*)
(*) + se
a declinação for do mesmo sinal da latitude (Norte ou Sul) , - no
caso oposto
Conhecida
a altura do Sol, através do Manual de Munique(*) era possível
obter a declinação (Cálculo da Declinação do Sol no tempo dos Descobrimentos)
e proceder ao cálculo da latitude obedecendo ao estipulado em várias regras
(Regimento) do referido manual. Na perspectiva da sua aplicação prática,
vejamos a aplicação de algumas das regras:
(*) - o
Manual de Munique é invocado apenas a título meramente exemplificativo da
aplicação de um determinado regimento, poderíamos ter utilizado, como exemplo
alternativo, o Manual de Évora ou outros ainda.
Regra nº1

Vamos
confirmar a aplicação desta igualdade e das suas condições.
Passo 1
Entre
doze de Março e 14 de Setembro (*), a declinação do Sol é Norte. Se
durante a passagem meridiana do Sol a sombra se projectar para norte
("se te fizer ao norte") isto significa que o observador se
encontra " a norte" do Sol, ou seja a declinação e a latitude são do
mesmo sinal.
(Recordamos que a 4 de Outubro de 1582, foram suprimidos dez dias ao
calendário, fazendo com que o dia seguinte fosse 15 de Outubro - reforma
Gregoriana)
Passo 2
A regra
do Manual de Munique estabelece que:
" tirarás
a altura que tomaste de noventa, e o que ficar ajuntarás à declinação "
Aplicando
a fórmula, temos então
Latitude = (90º - altura observada do Sol em relação ao horizonte) +
Declinação (mesmo sinal, Latitude e Declinação)
Continuando
com o Manual de Munique, vejamos agora a conclusão da aplicação da primeira
regra e a aplicação da segunda :

Passo 1
Se a
altura observada para o Sol é exactamente igual a 90 graus isso significa que o
paralelo (latitude) onde se encontra o navegador é exactamente igual à
declinação do Sol.
Aplicando
a fórmula, temos então
Latitude = (90º - altura observada do Sol em relação ao horizonte) +
Declinação (mesmo sinal, Latitude e Declinação)
Latitude = zero + Declinação = declinação
Passo 2
A regra
nº 1 do Manual de Munique, para ser aplicada, exige que o navegador se encontre
a norte do Sol quando a declinação deste é também norte (signos Áries, Touro,
Gemini, Câncer, Leo e Virgo),
"e
saberás que este regimento é verdade se a sombra vai para o norte "
Regra nº2
Passo 1
Entre
12 de Março e 14 de Setembro (em 1504), a declinação do Sol é Norte. Se
durante a passagem meridiana do Sol a sombra se projectar para Sul
isto significa que o observador se encontra " a sul" do Sol mas a
norte do Equador ("estando
do trópico de Câncer para a Linha "),
ou seja a declinação e a latitude são do mesmo sinal.
Passo 2
A regra
nº 2 do Manual de Munique estabelece que:
" ajuntarás
a altura que tomaste com a declinação, e o que sobejar de 90 é o que estás
afastado da linha "
Aplicando
a fórmula, temos então
Latitude = (90º - altura observada do Sol em relação ao horizonte) +
Declinação (mesmo sinal, Latitude e Declinação)
Regra nº3

Passo 1
As
regras 1, 2 e 3 assumem que o navegador se encontra a norte do equador
(linha). Entre 14 de Setembro e 12 de Março (em
1504), a declinação do Sol é Sul.
Passo 2
Identificada
a posição do Sol, aplicando a fórmula nossa conhecida, temos então
Latitude = (90º - altura observada do Sol em relação ao horizonte) -
Declinação ( Latitude e Declinação de sinal diferente)
que é
igual a
Latitude = 90º - (altura observada do Sol em relação ao
horizonte + Declinação )
A regra
estabelece que
"toma
a altura do Sol, como já disse, e olha nesta tabuada a declinação que o
Sol tem em aquele dia, e ajunta tudo; e o que for tira-o de 90"
confirmando
a absoluto a nossa pequena fórmula.
Regra nº4

Através
da publicação da 4ª regra, concluímos a nossa abordagem às regras constantes no
Manual de Munique. A 4ª regra estipula, para as situações em que o navegador se
encontra a Sul do Equador, que o regimento a utilizar seria o oposto do
utilizado caso o navegador se encontrasse a norte do equador.
Precisão do Cálculo da Latitude (séculos XV e XVI)
Ao
avaliar o grau de precisão nos cálculos acima explicados, podemos então afirmar
que o erro máximo no valor obtido para a declinação seria na ordem dos 24
minutos (leitura das tábuas sem interpolação -Cálculo da Declinação do Sol no tempo dos
Descobrimentos ). Se a este valor adicionarmos o
valor de 15 minutos, representando este o erro máximo na leitura da escala do
astrolábio ( Cálculo da
latitude através da altura do Sol), obtemos o valor de 39
minutos. Podemos então concluir o seguinte:
O erro máximo no cálculo da latitude através da altura do Sol, no final do
século XV e início do século XVI, considerando factores condicionantes tais
como as tábuas náuticas utilizadas nos cálculos para a declinação e os
instrumentos de leitura da altura do Sol, seria seguramente inferior a 45
minutos (45 milhas náuticas medidas em latitude), o que consideramos, tendo em consideração
os referidos factores condicionantes, como muito bom.
O grande mistério da longitude na
navegação
26-03-1762 D.C.
No dia 26 de Março de 1762, o grande
mistério da longitude foi resolvido quando um cronómetro que orientou com
sucesso o navio HMS Deptford de Portsmouth para a Jamaica.
Durante grande parte
da história, muitas mentes científicas tentaram encontrar um método para
determinar a longitude exacta, fundamental para descrever a cartografia e saber
da localização exacta na navegação oceânica.
No século 3 a. C, astrónomo
grego Eratóstenes propôs o primeiro sistema de latitude e longitude
para um mapa do mundo.
Até o século 2 a.C., Hiparco, um
astrólogo e astrónomo grego, propôs um sistema de determinação da longitude,
comparando a hora local e absoluto.
No século XI, o muçulmano erudito
Al-Biruni estabeleceu a moderna noção que o tempo e a longitude estão relacionados
ao conceito de que Terra girava sobre um eixo.
A partir daí, dezenas de cientistas,
de Galileu a Edmund Halley ou Nevil Maskelyne, buscaram um método preciso para
determinar a longitude.
Encontrar a latitude foi fácil: foi
calculada pelo uso dum quadrante e astrolábio para determinar a inclinação do
sol ou pelas estrelas. E determinar a longitude em terra também não
foi muito difícil em comparação com a tarefa no mar - em terra, os cientistas
tinham uma superfície estável, local confortável e a chance de repetir os
experimentos.
No mar, os navegadores eram pressionados para saber a sua
localização exacta longitudinal, o que muitas vezes causava desastres. Quando
um erro de navegação resultou em um acidente com o navio Scilly, em 1707, o
governo britânico estabeleceu um prémio de 20 mil libras para quem apresentasse
uma solução.
Um relojoeiro autodidacta chamado John Harrison acreditava que a
solução estava num dispositivo mecânico que poderia ser colocado em
navios, quando iam para o mar.
Harrison projectou e construiu um complicado
relógio marinho, com duas barras interligadas para suportar o balanço de um
navio no mar.
Em 1737, o dispositivo foi testado numa viagem a Lisboa.
O
relógio de Harrison indicava correctamente a posição do navio, mas não estava
satisfeito.
Harrison construiu então mais cronómetros marinhos, cada um ainda
com mais precisão. Uma cópia de sua invenção foi inclusive levada na
viagem do capitão James Cook, entre 1772-1774, que permitiu ao
explorador fazer as primeiras cartas sobre as Ilhas do Mar do Sul.
Apesar de
cumprir os requisitos para ganhar o prémio, o astrónomo real Nevil Maskelyne
não aceitou que o problema da longitude pudesse ser resolvido por meios
mecânicos e convenceu o conselho a não entregar o prémio ao relojoeiro.
Filho
de Harrison, William pediu ao Parlamento Europeu e até mesmo escreveu ao rei
George III, que examinou o relógio.
No final, Harrison recebeu um total 14.250
libras durante o tempo em que ficou empenhado na solução dos problemas
relacionados à longitude. Em 24 de Março de 1776, John Harrison morreu em
Londres aos 83 anos.
Apesar dos seu invento nunca ter sido padrão para a
navegação náutica, seu dispositivo abriu o caminho para a criação das
ferramentas modernas de navegação.